T-values and meaning

And as in uffish thought he stood...

What do we use numbers for? We use integers to count whole objects (eg automobiles) or whole amounts (eg age in years). However, we use real numbers (typically decimal) not to count, but to measure. If our job is to make things, we need real numbers to make them correctly. For analytical and not synthetic purposes, real numbers are only used to compare with each other. For example, we want to know if a new refrigerator will fit in the available space, so we measure them both with a tape ruler, and check that the measurements of 'A' (the fridge) do not exceed the respective measurements of 'B' (the space).  For this type of use, real numbers seem to have much greater accuracy than needed, eg in terms of decimal places. In fact, for the purposes of relative comparisons, the accuracy of real (ie floating point) numbers seems wasted, a case of technical overkill.  What is needed in this case is a different sort of number, one designed purely for comparisons, and not for measurement. 

Such a hypothetical number system exists, at least partly- they are called ordinal numbers. T-values are a special type of ordinal, in which a hybrid is formed between a logical (base 2) and a metric (eg base 10, but could be other types) number.  Please note that this is a different arrangement to the conventional set up (eg in a computer programming language), in which logical typing is seen as existing at the lower end of a continuum which includes numbers of larger (numerically greater) base at its upper end. With T-values, the operational (decision-theoretic, flow control) aspect, is regarded as quite separate* from the organisational (data-theoretic, memory structure) aspect.  

*As has been noted elsewhere in this document, the distinction, though perfectly clear de dicto (if you will) is somewhat muddied de re by the constant learning system (CLS) of the human mind/TDE emulation. 

Neural representation
Hughlings Jackson and other later researchers established empirically and beyond any reasonable doubt that it is 'movement and not muscles'* that are represented in cortical circuitry. Consider the thirty or so muscles of the hand. These are utilized in 'myriad combination' to represent a particular region of topical (ie subjectively targeted) space, as might be the various bits of a register in primary computer memory, although with considerably more accuracy.  Just as there are more significant and less significant bits in the computer memory cell, so the muscles of the hand, or of any other body part, govern a greater or lesser range of movement. Furthermore, they are hierarchically arranged, like the bits of the register, the MSB's determining the gross features, and the LSB's the fine features of the movement under consideration. 

Higher levels command the lower levels to stop, not to start. 
Hughlings Jackson was also the first to understand the way that the higher level circuits governed the lower level ones - they rule by veto. That is, the lower level circuits operate autonomically, ie without being commanded. The natural state of lower order circuits is one of self-excitation. When higher levels command the lower ones, they order them to stop, not to start. Jackson also understood only too well the design compromise that this represented- the benefit of faster motor response came at the cost of epileptic potentiality. Only a small change in neural power balance between upper and lower levels, such as a badly located lesion, is sometimes all that is needed to condemn the unfortunate subject to a lifetime of epileptic fits of greater or lesser frequency and intensity.

By inspection, we see that neural circuits and not individual neurons are the means of storing and transmitting key computational values (T-values).  Such circuits represent variable, real number values as setpoint/thresholds, but they simultaneously express logic conditions and states by being switched on and off (true and false)- that is, they encode the finite states in deterministic automata. The 'variable value' part applies because, whatever the adaptive mechanism, neurons are 'plastic', ie their transfer function (expressed vaguely as output-per-input) is not fixed, that is it varies. Whether the mechanism causing this variation is a variable strength synapse or variable bias control input doesn't matter at this point (these are the two most popular options). 

What does matter is the end result - a finite network of causally interconnected states, where the causal connection with the self-in-world ('subject') experience arises because of the systematic nature of these variations - see figure 27(b)-
(a) their relationship to perceptual (external) and conceptual (internal) events, ultimately resolved by semantic (paradigmatic) grounding of symbols; 
(b) their relationship to each other, which is covered by computational syntagmatics. 

These two terms, paradigmatic and syntagmatic were first introduced into linguistics by Ferdinand Saussure, and have the same broad meaning as 'semantic' and 'syntactic' respectively. The idea behind the terms 'paradigmatic' and 'semantic' is that of a set of computational-linguistic-representational states which share a group of material  (physical, perceptual, analytic) and/or phenomenal (mathematical, conceptual, synthetic) properties. In other words, they are representative tokens of 'type', or 'class'. A group of perceptual (ie sensory) events is significantly matched ('thresholded') to a pattern stored in memory, which activates a matching predicate state in working memory. 

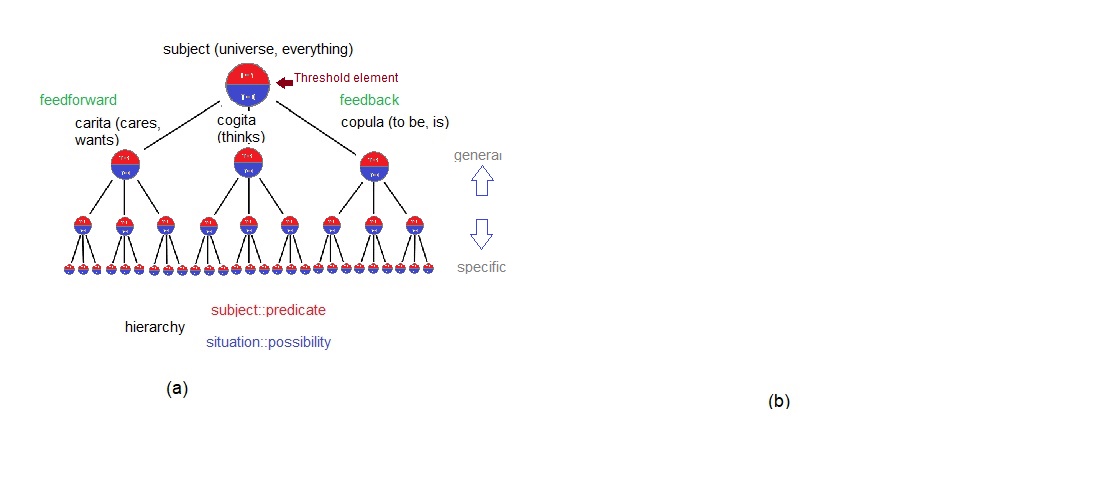
These predicate states are recursive and therefore hierarchical. Every perceptual grouping matches the top-most predicate ('everything', 'self'). This subjective 'root' state can be likened not to a noun but to the reflexive existential verb, to be, namely "I am". Strictly speaking, this is analogous to neither a verb  (process) nor a noun (structure), but to both. This is the top-most state in the GOLEM diagram - see figure 26(a).

*Phillips, C.G. Prof. (1973) Cortical Localization and 'Sensorimotor Processes' at the 'Middle Level' in Primates. Proc. Roy. Soc. Med. 66 Hughlings Jackson Lecture

Meaningful content, like description, need not be precise but must suffice

In the case of money, you can pay too much for a product or service, but you can never pay too little, because if your offer drops below the asking price, a 'no sale' results.  T-values are an appropriate number system to use for both meaning in minds and money in marketplaces, because they have built into them the concept of 'upward hierarchical entailment', by virtue of the ability to encode superveiling inequality, which is a sufficing (subset) relation. Upward entailment is of interest to grammarians  and linguists who must consider situations like the following:-
'Some' is upward entailing in its both arguments.
Ex:- Some student is Italian and blond. --> Some student is Italian.
But what about this case-
'No' is downward entailing in its both arguments. 
Ex:- No student is Italian. --> No student is Italian and blond.

Downward entailment can easily be transformed into upward entailment, and vice versa, by using a standard conversion of the universal quantifier.  We can convert the downward entailment in thelast case into its upward form by substituting 'All...not' for 'No'.
eg  Each student is not both Italian and blond ---> {upward entails} --> Each student is not Italian.

*The logician C. S. Pierce made a comprehensive study of signs, the carriers of meaning. He called this study 'semiology', but these days, the usual term is 'semiotics'. 

**https://mamori.com/semantics/0507.pdf  This is quite a useful introduction to logical entailment. However, it is incomplete as far as the 'each' quantifier goes.

We are now in a position to introduce T-values, which implement the ordinal* logico-numeric subsystem used by the TDE. A T-value substrate is not a necessary part of the TDE/GOLEM theory (TGT).  Without T-values, TGT is still perfectly able to implement subjectivity (psychophysics, qualia, introspection), both consciousness and self-consciousness, language and behaviour. But the TGT 'cog' thus constructed would be frozen in time, and unable to learn new stuff. Thus TGT without T-values is theoretically important (after all, it constitutes strong-AI at a level that has never been done before), but practically useless, since one of the main things one would want such an advanced AI to do immediately is machine learning!

A T-value is a truly semantic variable. It represents what Al Newell originally meant by a symbol, one that has implicit semantics. It has both presence (it participates, or does not participate in ongoing logical computations) as well as magnitude (when it is present, it participates in adaptational processes -ie learning). It consists of both logical and arithmetical facets, but these aspects are not independent of each other - compare the scalars that make up the (row, column) entries of a typical tensor matrix with the intertwined terms of a quaternion**. The operational part of a 'cog' is the more volatile, less permanent logical part which encodes the binary switching on and off of the predicates which form the upper levels of the cog's knowledge hierarchies. In contrast, the organisational part of the TGT cog is the less volatile, more permanent arithmetical part, involving those analog (real-valued) neural membrane bias thresholds which store lower-level (procedural, embodied) data.  At the lower levels, T-values devolve to conventional arithmetic cybernetics, ie with real-valued setpoints and saccadic step-sizes. At the upper levels, T-values devolve to conventional knowledge predicates (facts, either true or not). Figure 27 depicts these ideas. 

*Not to be confused with Alan Turing's PhD thesis (A. M. Turing  (1938) SYSTEMS OF LOGIC BASED ON ORDINALS;  A dissertation presented to the faculty of Princeton University in candidacy for the degree of Doctor of Philosophy) which dealt with ordinal SYSTEMS of conventional logic, and not ordinal LOGIC, as considered here.

**The Apollo moon missions could not have taken place without quaternions. Standard tensor analysis is fine for quantum mechanics, but quite useless in outer space. 

We are now in a position to see the truly revolutionary step that T-values represent. Lets recap- a biocognitive variable represented by a T-value will EITHER be zero, OR be equal to the currently set threshold value.  In figure 27(a) above, below the dotted line, T(y) = 0, whereas above the dotted line, T(y) = c. This is not like a fuzzy logic, where fractional truth values are used to achieve smooth operation (ie finite state transitions) with a relatively simple logic base (ie the number of premises is comparatively few in number). The 0..1 changes correspond to first order logic predicates. These changes are reactive that is, they are driven by global/superveiling feedback circuits. The switching events causing these changes are therefore deemed 'operational'. In contrast, the increments or decrements in the value of 'c' that occur as a result of learning mechanisms are feedforward in nature, ie they happen in advance of their intended use. These are therefore deemed 'organisational'. 

The overall effect of introducing T-values into a cognitive model is to turn the concept of a reflex on its head-

Reflexes are of the form-

The whole point of doing this is because the neural circuits in the lower echelons of the brain's hierarchies are switched 'on' by default, and therefore require a normalising inhibitory control circuit to achieve quiescence. To activate these neural circuits, one applies inhibition to the inhibitor (usually from above, ie from supervisory circuit levels), hence the term 'meta-inhibitory' is applied to this governance technique. WHEN they are turned on, each neuron's activation continues to increase until it reaches, then exceeds the threshold (y=c), where the output of the neuron is used to increase the bias (membrane) resting potential, causing a decrease in its actual voltage. This then turns the neuron down, in classic feedback style! 

The end result is the one that is desired- IF the neuron's circuit is activated, THEN the feedback circuit will maintain the neural bias potential very close to its threshold value y=s. In other words, IF (response r) THEN (stimulus s) ....QED. 

*perhaps a term like elsifex or selfexer could be used

T-values ( hereafter referred to as TV's) are the way that neurons, neural circuits, and neural networks represent the meaning and measure of engineering and psychophysical variables, for the purpose of  performing biocomputational functions. The context within which they perform these functions is that upper layers control lower layers by inhibition. That is, lower layers would be 'always on' if it wasn't for the inhibitory influence of the upper layers. When the lower layers must operate, the upper layers need only stop doing what they normally do, and the lower layers are then free to perform semantic transformations. For deliberate (voluntary) actions, however, meta-inhibition is used. 

TV's are like a vector with two components. Another analogy is to compare them to a complex number with real and imaginary parts? The operation of the human/mammalian biocomputer uses the logical part of the TV, while the organisational part uses the arithmetic part of the TV. Together, the two parts of the TV form an arithmetic-logical unit (ALU), just like any other computer.

The fact that our brains use a 'constant learning system' (CLS) means that both logical and arithmetic parts of the TV 'dyad' are being altered concurrently and each part cannot easily be analysed on its own. However, for the purposes of the exercise, imagine that our brains do not use a CLS. The temporary assumption is that the arithmetic values remain constant in between learning epochs, and the variations in the logical part can now be analysed.

Warren McCulloch* first imagined the branched neural networks in the brain to be pure logic processors. That is, the output lines of the neurons in each layer could take on either of the two Boolean values [0..1] , or equivalently {T,F}, depending on whether the (subjective, recursive..) logical predicate they were currently representing was true or false. Depending on each neuron's state of excitation or inhibition, a spanning sub-tree of the (initially feedforward) network would be selected for the current computation.  Of course, McCulloch did not specify how the neurons conductances would be set or changed. Ever since then, various researchers (Widrow-Hoff, Hebbs, Sejnowski etc) have designed the latest learning/update rule. In a way, TV's are really just the latest in a long line of candidates for this job.

In a non-recurrent feedforward network, the information flows only one way. Presumably, the network has hierarchical interconnections, otherwise it would violate the need for semantic consistency. This point is important. Without referential hierarchy, the nodes in the network lack a consistent way to map them to semantics (subject-predicate truth states). The moment to moment operation of the network is such that it BOTH (i) extracts the meaning of the network's bottom-up inputs, AND (ii) constructs the output 'message' (thought / behaviour) corresponding to the network's top-down intention. The former case (i) applies to the GOLEM input channel (right hand side as drawn) while the latter case (ii) applies to the GOLEM output channel (left hand side as drawn).  Described in this way, it is identical to the GOLEM, the TDE theory's memory process model. Conversely, the TDE fractal (TDE-R) is the GOLEM's computational architecture. Note the unusual pairing of the descriptors- one usually associates 'memory' with 'architecture', and expects 'computational' to occur with 'process'. The GOLEM expresses the linguistic (synto-semantic) nature of biocomputation while the TDE-R encapsulates its cybernetic (drive-state procedural) basis. This is the architectonic legacy of the pyramidal crossbar switches, a (feedforward) spatial x-bar switch in the cerebrum, a (feedback) temporal x-bar switch in the cerebellum. The presence of x-bar switching introduces recurrency (looping) into the semantic hierarchies.

TVs have an unusual property, which is exemplified by the denotation/connotation contrast (see figure/table 28). In a conventional computer science treatment, all three words in any row of this table would require a separate predicate, ie a separate node in the semantic hierarchy. Using TVs, each row is represented just once, with the three nuanced meanings encoded in small variations in the magnitude in the TV.

*McCulloch, W.S. & Pitts, W. (1990) A Logical Calculus of Ideas Immanent in Nervous Activity. Bull. Math. Biol. Vol. 52, No. l/2. pp. 99-115

Lets try to get a mental overview of the T-value system.  Firstly, all semantic computation requires at least one contextual hierarchy, so that 'conventional' ( 'absolute', 'non-relative') meanings can be encoded. Semantics (meaning) is not a local property, but a global one. That is, each node in the hierarchy can be said to 'mean' something only by virtue of its 'logical extension', or location within the data structure (a contextual hierarchy). Actually, when you think about it, the position of a point in a Cartesian coordinate system is a similar kind of thing. The point itself has no inherent or intensional meaning, its significance arises purely from its extension, or relationship to its defining framework, in this case the distances projected by the point on each of its (x,y...z) axes.  Mathematically, these points are represented by affine vectors. Another word for 'affine' is relative, they have meaning relative to the offset of the origin of the defining framework. Each MCP neuron is a graphic version of a typical affine point, which can also be expressed in so-called homogeneous, or scale-independent, coordinates. 

With the rare exception of onomatopoea, names and simple nouns in English, as well as many other languages, are arbitrarily given. There is nothing in the form of the name itself to suggest its referent, either a concrete object or abstract property*. Just like the point in space, its meaning is purely extensional, a consequence of its relative position w.r.t. the origin of the coordinate framework. 

It has been understood since classical times that meaning (eg of words and sentences) is relative. What is meant by 'relative' depends on context. Usually, what is meant is exactly the same thing that is meant by 'relative' in the Cartesian point example given above. The role of the origin of the Cartesian frame in traditional linguistics is played by the formal model (grammar and vocabulary) of the language.

Another meaning of 'relative' connotes the subtle 'bending' of the dictionary (denotative) meaning, as one stretches/relaxes a guitar string to inflect the base note (N) upward to its sharp (N#) or downwards to its flat (Nъ). The T-value system, with its dual encoding, can therefore be used to represent both a symbol's denotative (qualitative, non-relative) as well as connotative (quantitative, inflected) semantics.

Think of the basic semantic hierarchy as a field of semantic locations. These can be compared to the system of natural numbers (ie the positive integers). The most basic way to access a given number is to perform repeated additions, first one by one, then by larger steps. But doing arithmetic purely by means of addition would be much too cumbersome. Multiplication is a more powerful operation, yet is still semantically reducible to repeated additions. In a similar way, combined use can be made of the two parts of the T-value dyad, namely (1) its basic logical meaning, and then (2) its factored meaning or connotative relation. 

Topic - a non-truth-conditional part of semantics
Topic is the part of semantics that is not concerned with truth. Generally, in a Montague grammar, the structure of the sentence is <SUBJECT><Predicate> where predicate is defined recursively as follows-  <Predicate> := <Topic><Predicate>. In this viewpoint, <Topic> is a kind of subordinate <SUBJECT>. This is not surprising, considering the way these two words often substitute for each other in daily English use. 

In TGT, knowledge, facts and semantics (meaning) are semantic equivalents. The meaning of a sentence is equivalent to the additional (INTERsubjective) knowledge that it delivers to the receiver.  This knowledge is stored as a hierarchical field of nodes (meanings). Each possible semantic description matches some kind of  This means that what works for one works for the other two. Consider the TGT idea that beliefs are what knowledge is (potentially) made from. Beliefs form the feedforward stage of the knowledge UGP. This allows for a radical new idea- that it is beliefs (axiomatic possibility or truth-state) which likewise form the scaffolding/kindling for both meaning (semantics) and reasoning (intelligence). For something to be TRUE or FALSE it must first 'work', ie be a possible state of the world, a potentially real situation. 

*Mill, J.S. (1843) A System of Logic, Chpt 2 'Of Names'